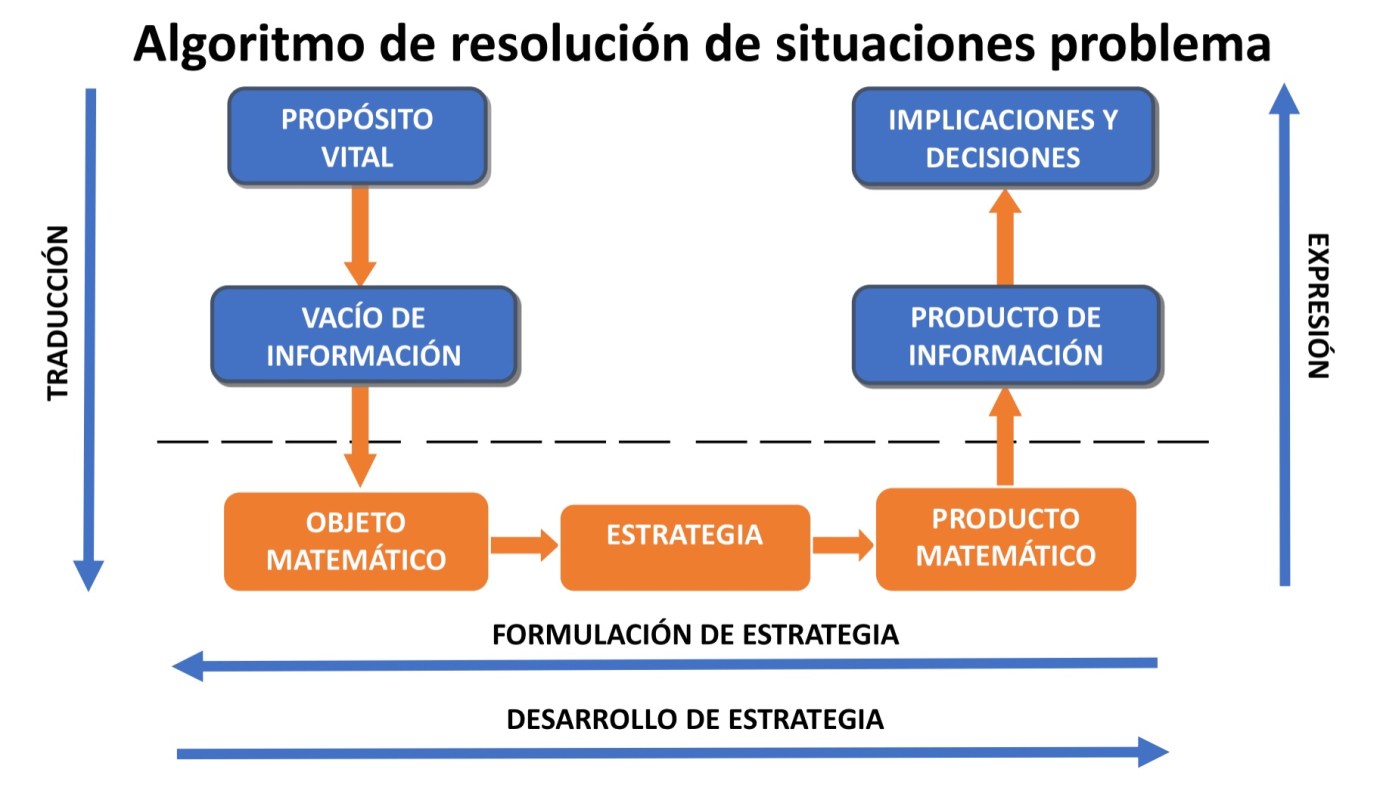
Esta es la segunda entrada de esta serie que presenta los cuatro procesos que componen el modelo teórico de las etapas de matematización de Matemáticas para la vida. En la entrada anterior se empezó describiendo el primer proceso: la traducción del vacío de información matematizable en un objeto matemático. Ahora, en esta entrada, se describirá el segundo proceso: la formulación de la estrategia, que recibe como insumo el objeto matemático determinado en el primer proceso.

En efecto, cuando se ha traducido el vacío de información matematizable en un objeto matemático, es necesario conocer el valor de dicho objeto, pues será este valor el que nos permita, luego, llenar el vacío de información. Para calcular este valor se debe formular una estrategia. Este proceso de formulación de la estrategia y el siguiente, el de desarrollo de la estrategia, están enmarcados en el mundo matemático, es decir, implican la puesta en juego de habilidades, conceptos y procedimientos específicos de las matemáticas. En cambio, los procesos de traducción del vacío de información y de expresión del producto matemático en la situación problema están enmarcados en el mundo matematizable. Lo anterior muestra que la competencia de matematización tiene un componente fundamental de cambios de representación entre diversos mundos o marcos de referencia. (Esto se puede ver gráficamente en el cambio de color, de azul a naranja, en la imagen que acompaña a esta serie de entradas. las partes azules corresponden al mundo matematizable y las partes naranjas al mundo matemático).

El proceso cognitivo de formulación de la estrategia tiene una característica particular: se realiza hacia atrás, por eso en la imagen se muestra como una flecha que va de derecha a izquierda. Esto se verá más explícitamente a continuación. El punto de inicio para formular la estrategia que permitirá calcular el valor del objeto matemático es justamente dicho objeto matemático. En matemáticas, cada objeto tiene uno o varios algoritmos que le son propios y que sirven para calcular su valor; algunos de estos algoritmos solamente están determinados por el objeto matemático, mientras que otros requieren no solamente la naturaleza del objeto, sino también los insumos que se hayan provisto para su cálculo.

Lo anterior se puede ilustrar con un par de ejemplos:

Si el objeto matemático en el cual se tradujo el vacío de información matematizable es, por ejemplo, la probabilidad de un evento simple, un método (algoritmo ) para calcularlo es dividir el número de casos favorables sobre el número de casos que tenga el espacio muestral. En este caso este método es inequívoco y corresponde directamente con el objeto matemático.

Ahora, si el objeto matemático es, por ejemplo, la hipotenusa de un triángulo rectángulo, entonces no hay un método único para calcularla, puesto que depende de los insumos que se hayan provisto en la situación. Así, si tenemos el valor de los catetos del triángulo, entonces podríamos usar el teorema de Pitágoras; pero si, en cambio, contamos con el valor de un cateto y un cierto ángulo diferente del recto, podríamos usar alguna de las razones trigonométricas.

Así, se puede entender que para formular la estrategia para calcular el valor del objeto matemático deben conocerse las características de dicho objeto y, en algunos casos, se debe hacer una relación con los insumos de la situación, de modo que se pueda encontrar el mejor método o algoritmo para calcular dicho valor.

En la entrada anterior se propuso un ejemplo, que se trae nuevamente a colación:

Camilo, un chef aficionado, está empezando su negocio de catering. Él está acostumbrado a cocinar sus menús para una pequeña cantidad de personas que de manera habitual le hacen pedidos, sin embargo y afortunadamente, un día una empresa le pide que elija y cocine un menú para 40 personas, un número mucho mayor al que regularmente atiende. Camilo elige un plato basado en papa, cuya receta indica que para cuatro personas debe usar dos papas tamaño jumbo. Como Camilo está empezando con su negocio, solo puede cocinar 15 papas al tiempo. ¿Podrá Camilo cumplir este pedido?

El objeto matemático de esta situación es la proporcionalidad, en específico, se debe calcular la cuarta proporcional conociendo la cantidad de insumos que se requieren para una receta correspondiente a un número inicial de personas y una nueva cantidad de personas para las cuales se va a preparar la misma receta. Un algoritmo que permite calcular la cuarta proporcional, determinado específicamente por el objeto matemático en este caso, es el conocido como regla de tres. En este sentido, el proceso cognitivo de formulación de la estrategia tiene el siguiente producto, mostrado en un diagrama estratégico:

El diagrama estratégico es un recurso metacognitivo que ayuda en la formulación de la estrategia. Está compuesto de tres partes: el producto, el método y los insumos, que se formulan en ese orden, es decir, en primer lugar, se formula el producto, que es el mismo objeto matemático en el que fue traducido el vacío de información matematizable; en este caso la cuarta proporcional. Luego se formula el método que, como ya se había dicho, en este caso es la regla de tres. Si el método tiene una fórmula, se puede hacer explícita en la correspondiente parte del diagrama estratégico; también se puede hacer explícito un procedimiento para calcular el objeto matemático. Por último, se formulan los insumos. Para hacerlo, se usa una especie de formato: magnitud matematizable: representación matemática = valor. En este caso, vamos a suponer que la receta original era para 4 personas y que el chef debe prepararla ahora para 40 personas y que la cantidad original de los insumos era 2 (por ejemplo, 2 papas). Esta manera de formular los insumos conecta el mundo matematizable con el mundo matemático.

Las matemáticas son un área de conocimiento muy propicia para ayudar a desarrollar el pensamiento estratégico y por eso es clave el proceso de pensamiento implicado en la formulación de la estrategia. Para terminar esta entrada, es conveniente hacer una anotación didáctica que puede ayudar a que este efecto se potencie. Es usual que en el ámbito escolar se propongan situaciones problema cuyos datos son todos insumos, es decir, no se ofrecen datos sobrantes a los estudiantes, lo cual hace que ellos simplemente hagan la operación que están aprendiendo en determinado periodo escolar sobre unos números que aparecen en la situación problema, sin entender muy bien de qué se trata lo que están haciendo. Por eso, en Matemáticas para la vida se suelen proponer situaciones problema con datos que no son insumos, a veces con características lejanas de la naturaleza de los insumos y otras veces con características cercanas, de modo que el estudiante deba hacer un trabajo de comprensión de lectura para separar los insumos de los datos.