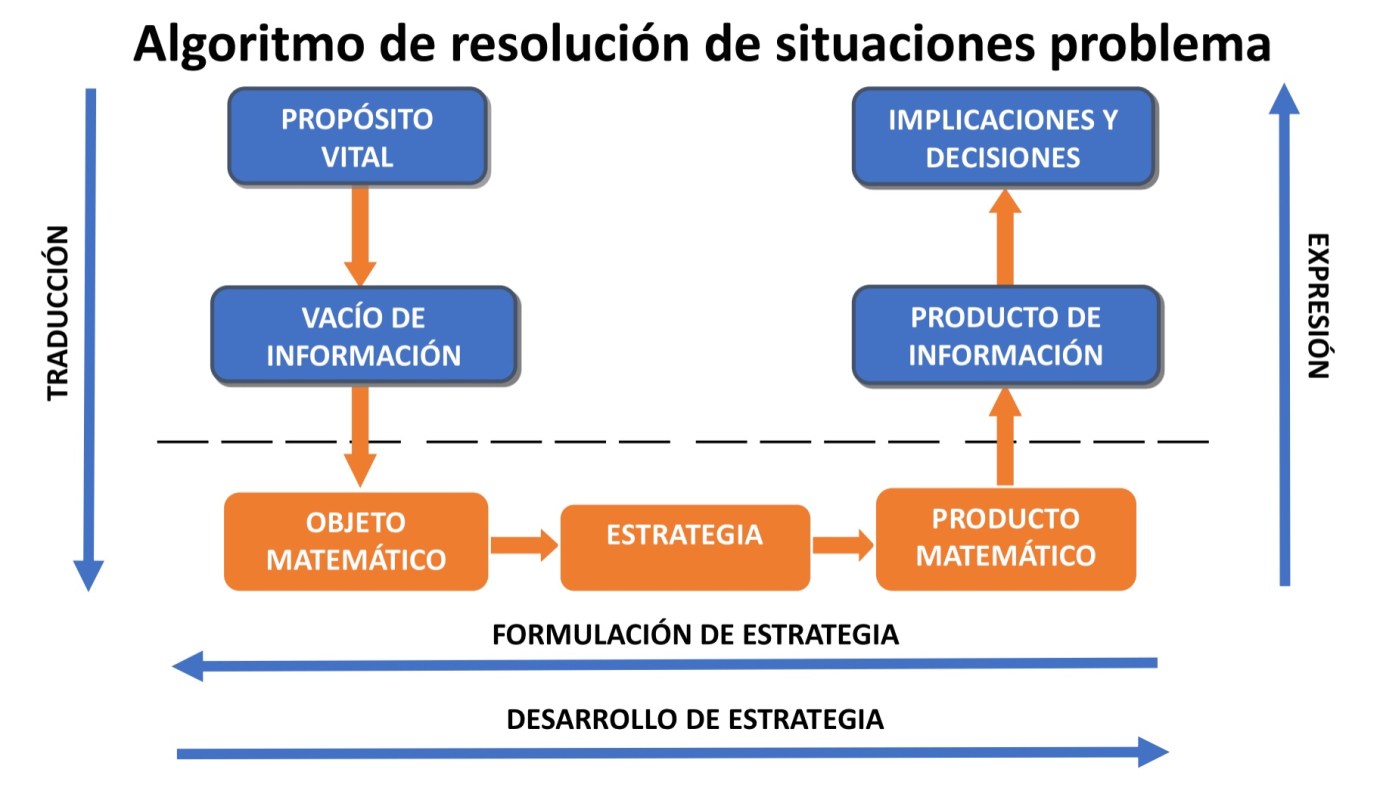
Esta es la cuarta y última de las entradas de esta serie en la que se describen los procesos de pensamiento involucrados en las etapas de matematización. En este punto es conveniente recapitular lo que se ha propuesto en las anteriores entradas de esta serie. Matemáticas para la vida pretende formar matematizadores de la realidad, es decir, personas que son capaces de identificar y resolver situaciones problema matematizables. Esta capacidad la tiene una persona cuando desarrolla cuatro procesos de pensamiento:

1. Identificar en la situación un vacío de información matematizable y traducirlo en un objeto matemático.
2. Formular una estrategia matemática para encontrar el valor del objeto matemático.
3. Desarrollar la estrategia formulada.
4. Expresar el valor del objeto matemático en términos de la situación problema, para tomar decisiones.

En las tres entradas anteriores hemos descrito los primeros tres procesos de pensamiento de esta lista; en esta entrada se describirá el último proceso.

Resolver una situación problema matematizable no implica únicamente encontrar un valor a partir de una serie de operaciones o de un algoritmo matemático. La situación problema nace de la necesidad que tiene un agente de alcanzar un propósito no necesariamente matemático y, en ese sentido, su solución debería estar orientada a alcanzar dicho propósito, por eso, un valor restringido al mundo matemático no resuelve la situación. Sin embargo, este valor es el insumo para realizar dos acciones:

1. Llenar el vacío de información matematizable que se formuló en el proceso de traducción.
2. Tomar decisiones o predecir implicaciones para la situación problema con base en el valor del objeto matemático.

Desde el punto de vista didáctico, los docentes debemos ser capaces de formular situaciones problema que tengan suficiente información para que, junto con el valor del objeto matemático, se puedan realizar las acciones anteriores. Es decir, una situación problema que únicamente interroga por un dato no deja el espacio para que los estudiantes puedan integrar información en la toma de decisiones.

En esta serie de entradas se ha desarrollado el siguiente ejemplo:

Camilo, un chef aficionado, está empezando su negocio de catering. Él está acostumbrado a cocinar sus menús para una pequeña cantidad de personas que de manera habitual le hacen pedidos, sin embargo y afortunadamente, un día una empresa le pide que elija y cocine un menú para 40 personas, un número mucho mayor al que regularmente atiende. Camilo elige un plato basado en papa, cuya receta indica que para cuatro personas debe usar dos papas tamaño jumbo. Como Camilo está empezando con su negocio, solo puede cocinar 15 papas al tiempo. ¿Podrá Camilo cumplir este pedido?

En la entrada anterior se calculó el producto de la estrategia, la cuarta proporcional, y se obtuvo un valor de 20. En este momento del proceso es necesario expresar este valor en términos de la situación problema para llenar el vacío de información (la cantidad de insumos, en este caso papas, para determinado plato), por lo tanto, se puede decir que Camilo requiere 20 papas para elaborar el plato que ha elegido para 40 personas. Este es un primer momento de la expresión del valor del objeto matemático en la situación problema.

Un segundo momento, más profundo y productivo, nace de dar solución a la situación problema. En el caso del ejemplo que se viene trabajando, se podrían proponer implicaciones, como que Camilo requeriría un mayor tamaño de ollas y de fogón para cocinar ese número de papas o tendría que hacerlas en varias tandas, que debería considerar que este pedido se añade a sus pedidos ordinarios, etc.

Este último proceso enriquece la motivación de los estudiantes para usar las matemáticas y sentir que tienen poder cuando las aplican, reforzando la sensación de autoeficacia, indispensable en el proceso de aprendizaje.