Matemáticas para la vida propone cuatro etapas para el desarrollo del pensamiento matemático. La tercera de estas etapas se denomina segundo nivel de abstracción, y es un momento dedicado al desarrollo de pensamiento algebraico y al aprendizaje del álgebra que, entre otras utilidades, es clave para la comunicación de las ideas matemáticas. Esta es la primera de una serie de entradas dedicadas a describir los modelos (teórico y didáctico) que enmarcan esta etapa.

Abstraer es un proceso cognitivo que nos permite aislar las características esenciales de un objeto, es decir, eliminar de nuestra consideración los rasgos circunstanciales o accesorios. El proceso de desarrollo del pensamiento que propone Matemáticas para la vida tiene cuatro etapas, dos de las cuales son momentos dedicados a (o con gran énfasis en) la abstracción.

La primera de estas etapas de abstracción ocurre al inicio del desarrollo del pensamiento matemático e, idealmente, tiene lugar hasta los 6 o 7 años, sin embargo, esto es relativo porque depende de factores como las condiciones particulares de los estudiantes y del entorno escolar en el que se encuentren. En esta etapa se busca que las personas abstraigan objetos de la realidad sensible en objetos matemáticos, es decir, que aprendan a ver las características matemáticas del mundo que las rodea, características como: la noción de cantidad, la noción de forma, la noción de posición, la noción de magnitud, la noción de patrón, etc. y que aprendan a realizar procesos de pensamiento matemático con base en estos objetos, procesos como: contar, predecir, medir, ubicar(se), describir, etc. Con base en esta etapa, los estudiantes viven después una primera etapa de matematización, que se caracteriza, aunque no exclusivamente, por que en ella se resuelven situaciones problema que no integran objetos matemáticos de diferentes ejes de pensamiento.

El segundo momento de abstracción se lleva a cabo después de esa primera etapa de matematización y, como ya se dijo, tiene como objetivo el desarrollo del pensamiento algebraico. En esta etapa la abstracción ocurre entre elementos de la geometría y elementos del álgebra, es decir, se busca que los estudiantes abstraigan nociones geométricas en objetos algebraicos.

Como cada una de las etapas para el desarrollo del pensamiento matemático que propone Matemáticas para la vida, este segundo momento de abstracción está descrito también por un modelo teórico, que contiene los procesos de pensamiento que se desarrollan en los estudiantes, y por un modelo didáctico, que prescribe las interacciones que deben darse entre profesor y estudiantes para que ocurra el desarrollo de dichos procesos. En este caso, más que un conjunto de procesos, el modelo teórico se presenta como una trayectoria de aprendizaje.

Pero antes de presentar el modelo teórico de esta etapa, es importante hacer claridad que la abstracción se da de manera gradual en tres niveles (que se repiten en forma de ciclos): concreto, gráfico y simbólico. En el nivel concreto se realizan actividades de manipulación, reconocimiento, descripción y relación de las formas geométricas: puntos, líneas, polígonos y poliedros. En el nivel gráfico se representan mediante dibujos las piezas concretas. Y en el nivel simbólico se hace otro cambio de representación, esta vez a símbolos algebraicos.

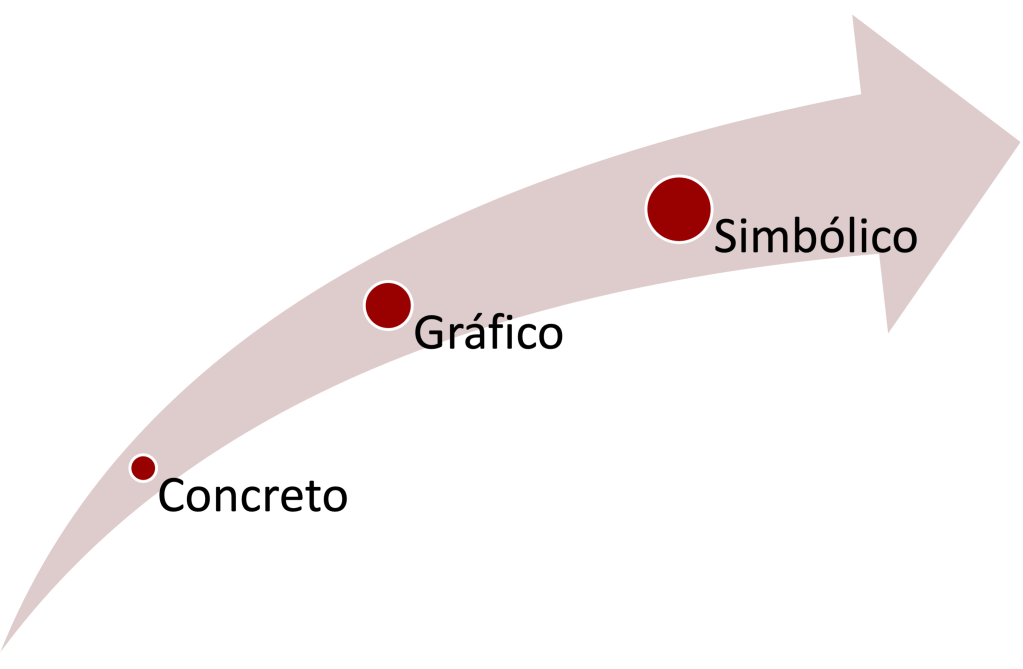
Estos cambios de representación se basan en lo propuesto por Bruner (1964), quien considera que «los procesos cognoscitivos del pensamiento humano y del aprendizaje se ven fuertemente influenciados por tres modos de representación que posibilitan identificar cómo se van representando mentalmente los conceptos e ideas que se aprenden». 

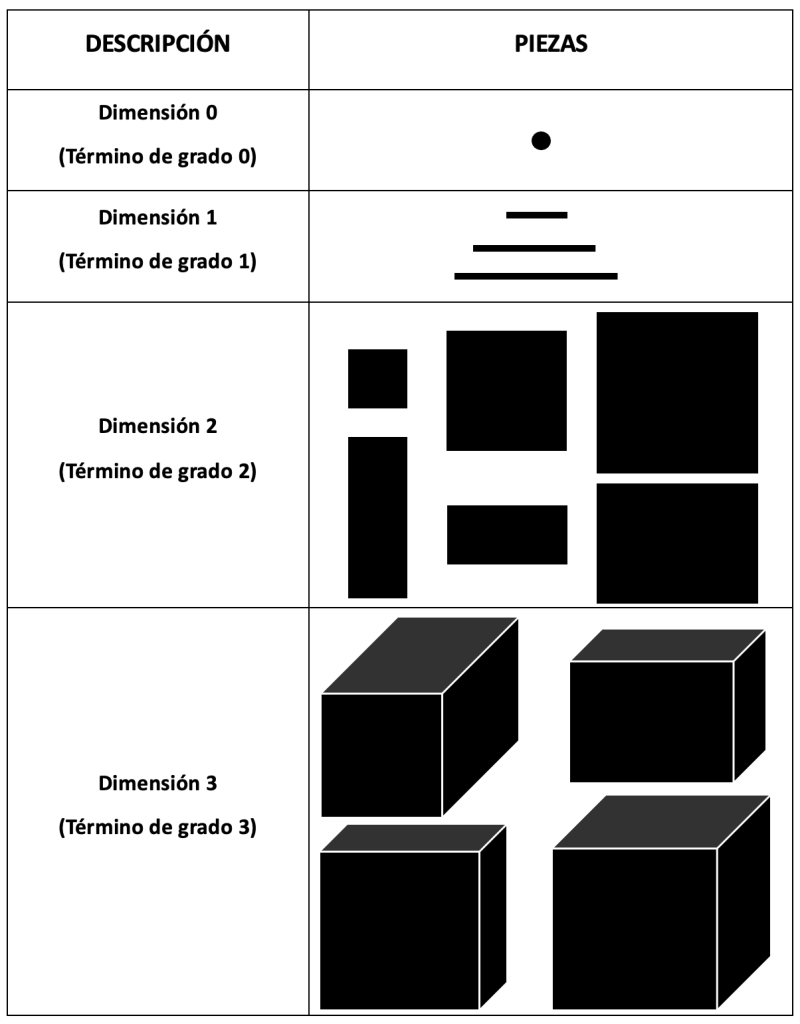
Para trabajar en esta etapa de abstracción se usa material concreto conformado por piezas geométricas. Algunas de estas piezas se pueden ver en la siguiente tabla:

En una próxima entrada se describirá en detalle el modelo teórico de esta etapa del desarrollo del pensamiento matemático.