En la entrada Las etapas del desarrollo del pensamiento matemático, se presentaron de manera somera los propósitos y características de las cuatro etapas que sigue Matemáticas para la vida para procurar un adecuado desarrollo del pensamiento matemático. También, se indicó que cada una de estas etapas se describe a través de un modelo teórico y un modelo didáctico. Ahora, en la serie de entradas que comienza con esta se presentará el modelo teórico de las etapas de matematización (la primera y la segunda) y dado que el modelo teórico describe los procesos de pensamiento que se desarrollan en cada etapa, presentar este modelo es equivalente a presentar dichos procesos.

Antes de empezar a describir estos procesos, conviene recordar el concepto de matematización. La matematización es una competencia (un saber hacer en un contexto) por medio de la cual una persona reconoce una situación matematizable, la modela en un objeto matemático, propone una estrategia para encontrar el valor de dicho objeto matemático y, por último, usa esta información para tomar decisiones en la situación original. Es decir, que la matematización es la competencia que le permite a las personas interactuar con el mundo matematizable (el mundo de las situaciones susceptibles de ser modeladas en objetos matemáticos).

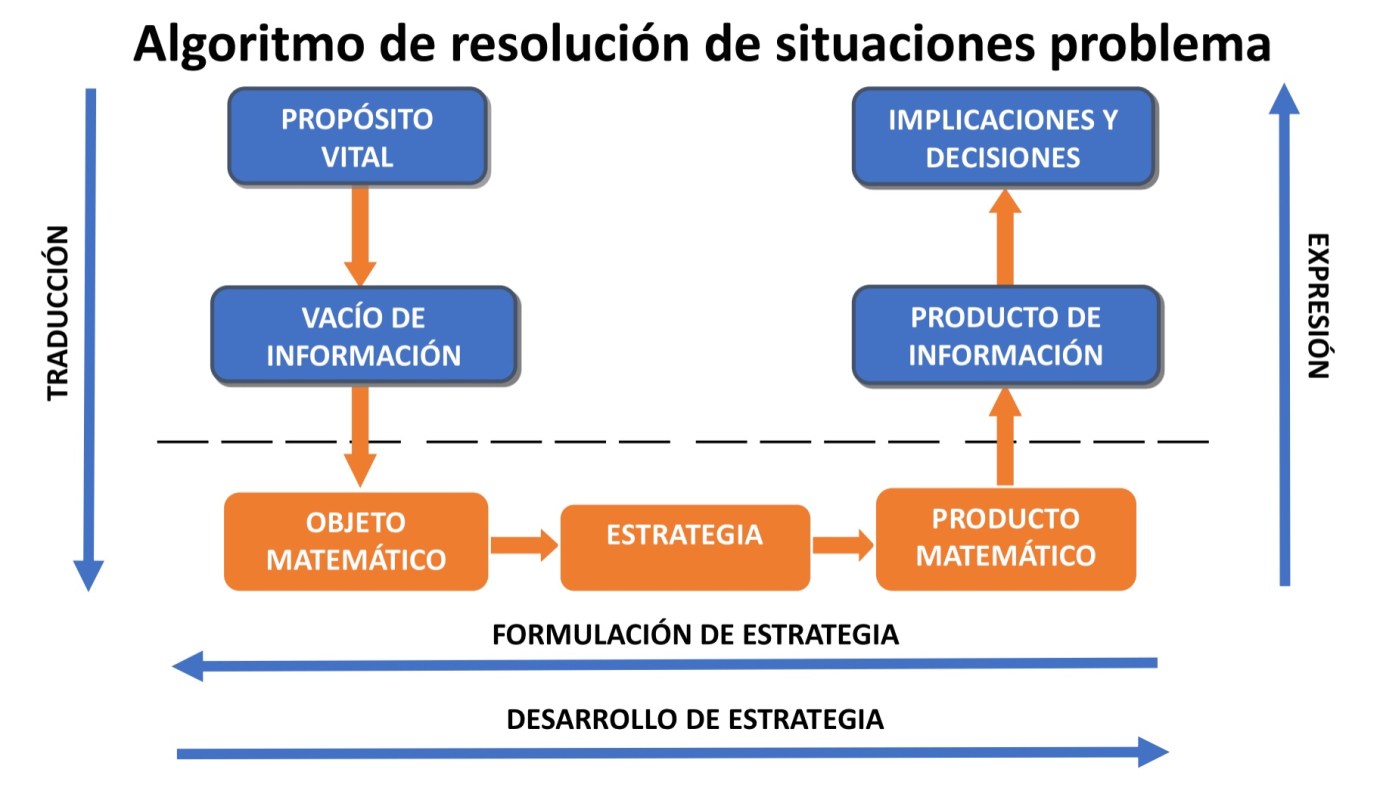
La competencia de matematización está compuesta por cuatro procesos que se enuncian a continuación (usando los nombres que se les han asignado desde Matemáticas para la vida):

• Traducir el vacío de información matematizable en un objeto matemático.
• Formular una estrategia que permita hallar el valor del objeto matemático.
• Desarrollar la estrategia para hallar el valor del objeto matemático.
• Expresar el valor del objeto matemático en términos de la situación problema matematizable.

El primer proceso de pensamiento implica el reconocimiento de la existencia de una situación problema matematizable, en la que un agente tiene un propósito vital, una necesidad (no necesariamente matemática) que resolver. Esta situación da lugar a uno o varios vacíos de información, alguno de los cuales tienen un carácter matematizable (nuevamente, susceptible de ser traducido a un objeto matemático). Específicamente, este primer proceso permite modelar matemáticamente la situación problema.

Un ejemplo puede ayudar a comprender mejor este proceso:

Camilo, un chef aficionado, está empezando su negocio de catering. Él está acostumbrado a cocinar sus menús para una pequeña cantidad de personas que de manera habitual le hacen pedidos, sin embargo y afortunadamente, un día una empresa le pide que elija y cocine un menú para 40 personas, un número mucho mayor al que regularmente atiende. Camilo elige un plato basado en papa, cuya receta indica que para cuatro personas debe usar dos papas tamaño jumbo. Como Camilo está empezando con su negocio, solo puede cocinar 15 papas al tiempo. ¿Podrá Camilo cumplir este pedido?

La anterior es una situación problema matematizable en la que un agente (Camilo) tiene un propósito vital (cocinar un menú para una mayor cantidad de personas de las está acostumbrado). Para resolver esta situación, a Camilo le pueden surgir varios vacíos de información, como: ¿cuál menú va a cocinar?, ¿cuánta cantidad de insumos debe conseguir? , ¿cómo va a ser la presentación de los platos que va a servir?, etc. Algunos de estos vacíos de información son de carácter matematizable y otros evidentemente no. Por ejemplo, el asunto relacionado con la presentación de los platos no es matematizable, pero la cantidad de insumos necesarios sí lo es.

Sí se elige el vacío de información relacionado con la cantidad de insumos para determinado plato, se puede notar que es de carácter variacional, ya que implica una labor de predicción. Y dentro de lo variacional, este vacío de información implica la relación entre razones de cambio discretas, o sea que está enmarcado en el objeto matemático de la proporcionalidad.

Así las cosas, se ha puesto en práctica el primer proceso, traduciendo un vacío de información matematizable (la cantidad de insumos para preparar la cantidad de platos solicitada de determinado menú) en un objeto matemático (proporcionalidad).

La traducción que se realiza en este proceso está apoyada por un instrumento llamado Mentefacto de contextos matemáticos que, a partir de las características del vacío de información, ayuda a encontrar el objeto matemático más acorde que lo traduce.