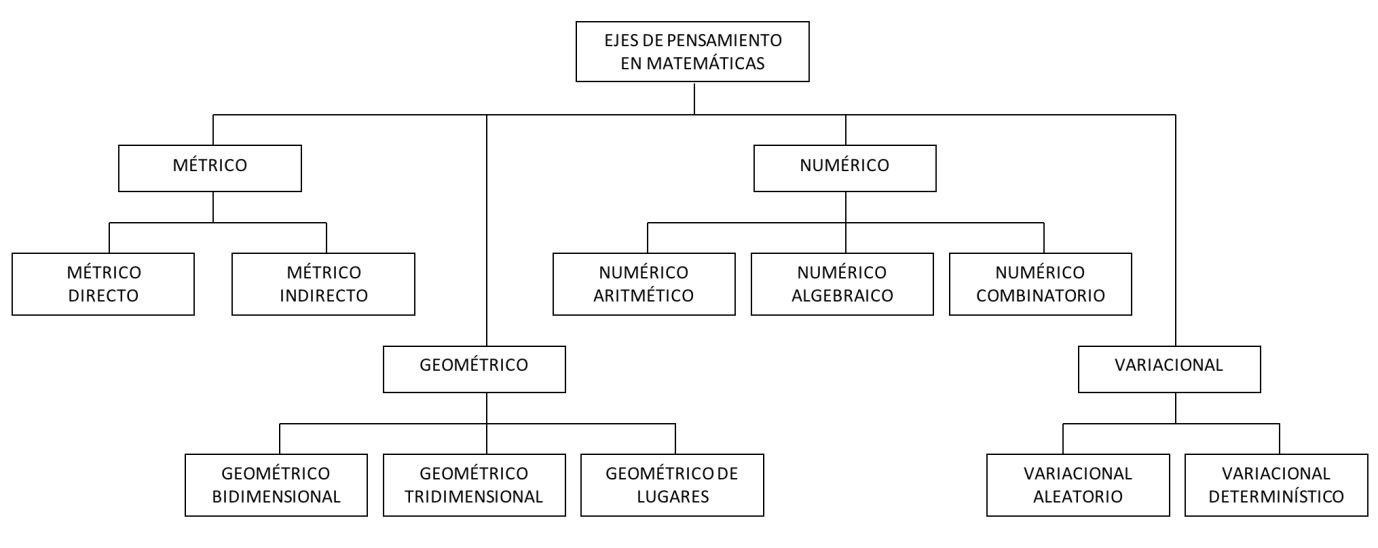
Matemáticas para la vida propone cuatro etapas para el desarrollo del pensamiento matemático. La tercera de estas etapas se denomina segundo nivel de abstracción, y es un momento dedicado al desarrollo de pensamiento algebraico y al aprendizaje del álgebra que, entre otras utilidades, es clave para la comunicación de las ideas matemáticas. Esta es la primera de una serie de entradas dedicadas a describir los modelos (teórico y didáctico) que enmarcan esta etapa.
Sigue leyendo
Los seres humanos desarrollamos la capacidad de pensamiento por necesidad. Nuestras actuaciones en los diferentes entornos, desde los primeros tiempos de la humanidad, han requerido que pongamos en juego (y, por ende, desarrollemos) nuestras capacidades cognitivas. El pensamiento matemático, al ser un tipo de pensamiento, también se ha desarrollado y se sigue desarrollando a partir de las necesidades. En esta entrada, se describen las necesidades que dieron y dan origen al desarrollo del pensamiento matemático y una forma de organizarlas.
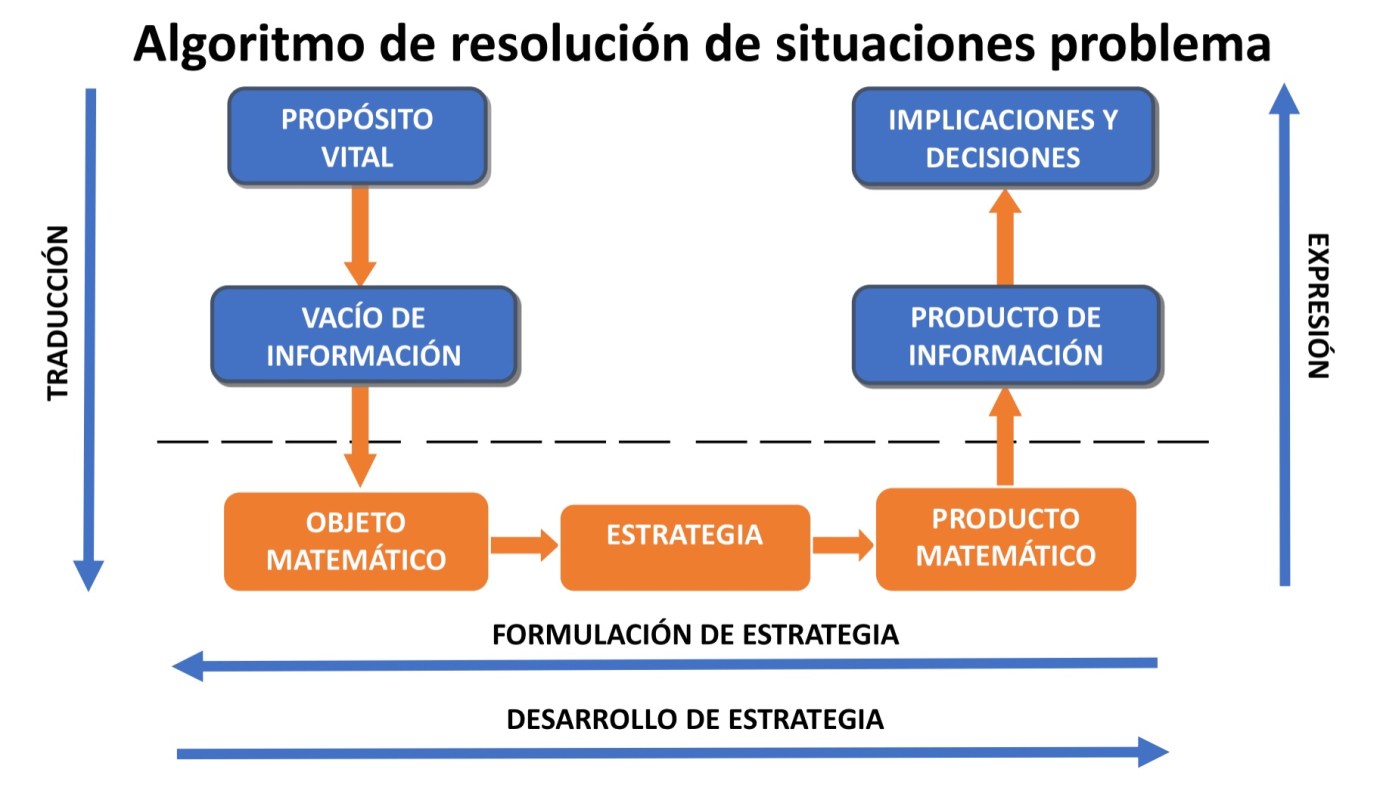
Sigue leyendoUno de los principales propósitos de Matemáticas para la vida es que los estudiantes aprendan a matematizar su realidad y, para esto, las situaciones problema matematizables son un recurso fundamental. En esta entrada profundizaremos en las características y en la construcción de este recurso.
En nuestra anterior entrada, mostramos las características de las situaciones problema matematizables: los recursos fundamentales para proponer, de forma didáctica, el proceso de matematización. En esta entrada resolveremos una situación para ejemplificar dicho proceso.
En entradas anteriores hemos hablado de la resolución de situaciones problema matematizables, pero no las hemos definido, ni dado un ejemplo. Este es el propósito de esta entrada.
Matemáticas para la vida 