En la primera entrada de esta serie dedicada a describir una trayectoria de aprendizaje para el desarrollo del pensamiento algebraico se presentó un elemento fundamental: el cambio entre las representaciones concreta, gráfica y simbólica. También se mostraron algunas de las piezas concretas que se usan en la implementación de esta trayectoria. En esta entrada se presentará el modelo teórico de esta etapa de desarrollo del pensamiento matemático.
Sigue leyendo
Matemáticas para la vida propone cuatro etapas para el desarrollo del pensamiento matemático. La tercera de estas etapas se denomina segundo nivel de abstracción, y es un momento dedicado al desarrollo de pensamiento algebraico y al aprendizaje del álgebra que, entre otras utilidades, es clave para la comunicación de las ideas matemáticas. Esta es la primera de una serie de entradas dedicadas a describir los modelos (teórico y didáctico) que enmarcan esta etapa.
Sigue leyendo
Todas las entradas que se publican en este blog contienen elementos desarrollados con base en el paradigma de educación matemática llamado Matemáticas para la vida. ¿En qué consiste este paradigma?
Sigue leyendo
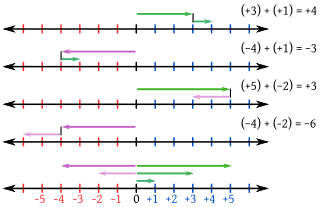
Aunque el título de esta entrada puede ser criticable porque suena a juego de palabras para captar la atención (… que también es la intención de un título), quiero dejar claro que tiene toda la intención de mostrar que el aprendizaje de los números negativos (es decir, del conjunto de los números enteros) puede ser un asunto interesante y agradable para estudiantes y profesores. Veamos por qué.
En nuestra entrada anterior describíamos, a manera de sobrevuelo, la secuencia didáctica que usa Matemáticas para la vida para formar matematizadores de la realidad.
En esta entrada vamos a profundizar en la primera de las tres fases de esta secuencia: la construcción del objeto matemático.
Hay muchas opciones para orientar el proceso de enseñanza-aprendizaje de los objetos matemáticos: a través de la resolución de problemas, la utilización del libro y su contenido, la presentación de los algoritmos asociados a los objetos o el uso de las TICs, entre otras. ¿Cuál será la mejor opción en cada caso?
Matemáticas para la vida 