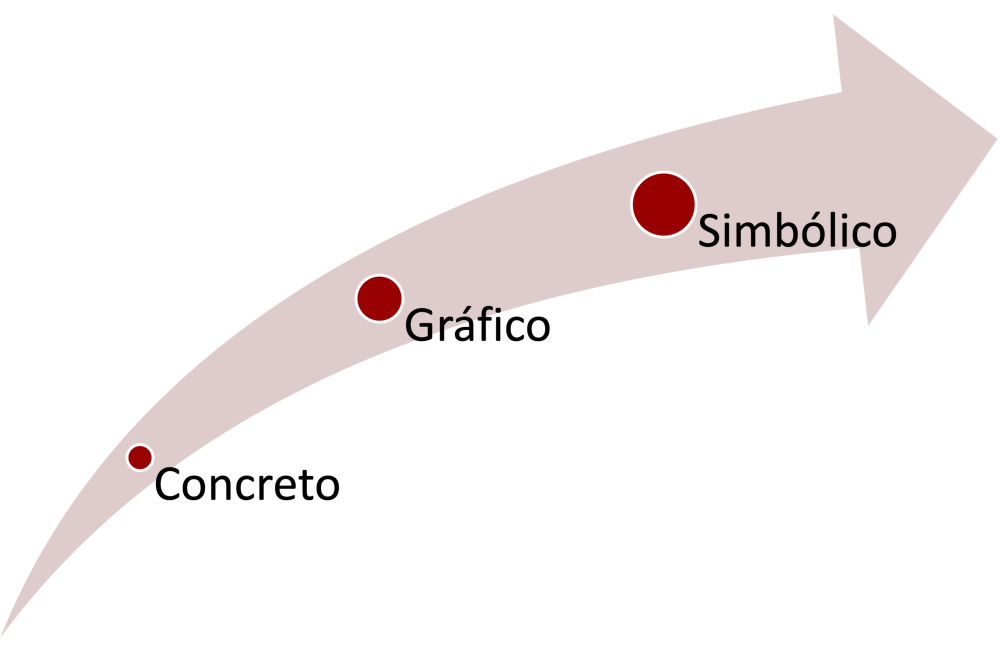
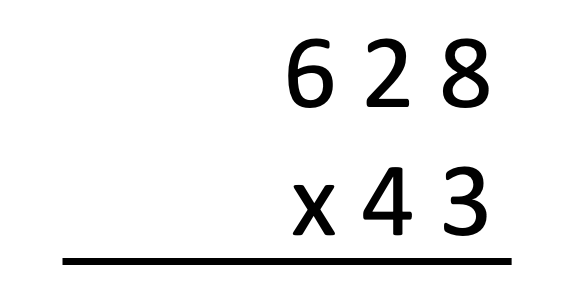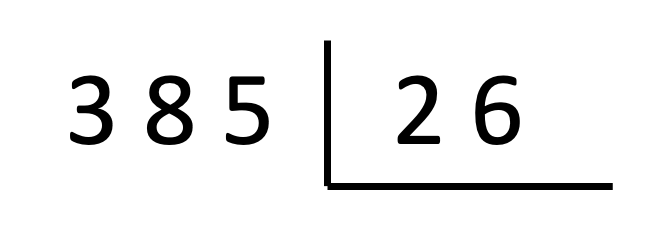En la primera entrada de esta serie dedicada a describir una trayectoria de aprendizaje para el desarrollo del pensamiento algebraico se presentó un elemento fundamental: el cambio entre las representaciones concreta, gráfica y simbólica. También se mostraron algunas de las piezas concretas que se usan en la implementación de esta trayectoria. En esta entrada se presentará el modelo teórico de esta etapa de desarrollo del pensamiento matemático.
Sigue leyendo
Matemáticas para la vida propone cuatro etapas para el desarrollo del pensamiento matemático. La tercera de estas etapas se denomina segundo nivel de abstracción, y es un momento dedicado al desarrollo de pensamiento algebraico y al aprendizaje del álgebra que, entre otras utilidades, es clave para la comunicación de las ideas matemáticas. Esta es la primera de una serie de entradas dedicadas a describir los modelos (teórico y didáctico) que enmarcan esta etapa.
Sigue leyendo
La pregunta que se hace en el título de esta entrada tiene una respuesta intuitiva: sí, debe haber más formas.
Sigamos adelante y veamos una forma ‘diferente’ de hacer multiplicaciones y, más importante, de entender bien.
Creo que estamos de acuerdo en que la división es una de las operaciones que más dificultades ocasionan a los estudiantes. Pero no es solamente el algoritmo de la operación lo que causa la dificultad, sino también su naturaleza. Por eso, Matemáticas para la vida usa una didáctica y un algoritmo particulares para la división.
Sigue leyendo
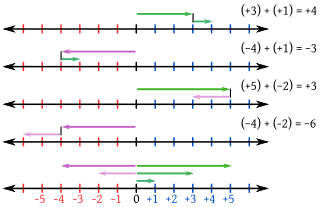
Aunque el título de esta entrada puede ser criticable porque suena a juego de palabras para captar la atención (… que también es la intención de un título), quiero dejar claro que tiene toda la intención de mostrar que el aprendizaje de los números negativos (es decir, del conjunto de los números enteros) puede ser un asunto interesante y agradable para estudiantes y profesores. Veamos por qué.
En días pasados estuve enseñando matemáticas a mi sobrina, más específicamente estuve enseñándole trigonometría. Ella es una persona especialmente curiosa e inteligente (habló el tío orgulloso), y por eso quise mostrarle este campo de las matemáticas antes de que se lo enseñaran en su colegio. En esta entrada les cuento cómo lo hice.
Uno de los principios de Matemáticas para la vida habla sobre la optimización de los algoritmos. En esta entrada ilustro este principio en el caso de la resta y de paso muestro una forma de restar que simplifica el aprendizaje de esta operación, que es (tal vez) el primer dolor de cabeza en el aprendizaje de las matemáticas. Sigue leyendo
Esta pregunta es, tal vez, una de las que más se han hecho en la historia moderna de la humanidad, a la que también se han dado numerosas respuestas.
En esta entrada del blog quiero compartir algunas ideas que han dado resultados, según nuestra experiencia, para el aprendizaje de la tablas de multiplicar en Matemáticas para la vida. Sigue leyendo
Imaginemos que estamos en una clase, al final de un periodo escolar en el que hemos enseñado el tema de la multiplicación. En esa clase tenemos planeado proponer a los estudiantes algunos problemas. Al entregar el taller, un estudiante se nos acerca y nos interpela: «ya leí el primer problema, ¿qué tengo que hacer?». Sin darnos tiempo de responder, una compañera le contesta: «pues, ¿qué crees que tienes que hacer?… estamos viendo multiplicación. ¡Multiplica!»
En ese momento no sabemos qué hacer… ¿está bien la respuesta de la estudiante? ¿o estábamos esperando otra cosa? Veamos la propuesta de Matemáticas para la vida para tratar esta situación.
Esta es la quinta y última entrada de esta serie sobre la secuencia didáctica que Matemáticas para la vida usa para que los estudiantes aprendan a resolver situaciones problema matematizables.
Esta entrada está dedicada a la última fase de esta secuencia: el desarrollo de la competencia.
Matemáticas para la vida 