Tradicionalmente, la enseñanza de las matemáticas está organizada con base en temas. Así, durante el avance de un estudiante por su etapa de formación en matemáticas básicas, comienza aprendiendo temas de la aritmética, luego aprende contenidos relacionados con el álgebra, más adelante viene la trigonometría y, normalmente, se termina el bachillerato con los temas de cálculo. La geometría y la estadística se enseñan paralelamente a estas áreas que he mencionado, aunque como lo reportan no pocos estudios, son dos áreas que se menosprecian durante la formación escolar. En Matemáticas para la vida el énfasis se pone en desarrollar el pensamiento matemático de los estudiantes y, por lo tanto, se basa en otra organización.

Esta organización tiene su origen en considerar no a los contenidos, sino a los procesos de pensamiento como sus tensores. Es importante aclarar que los contenidos tienen un papel importante dentro del modelo, pero no son el factor curricular central.

Matemáticas para la vida propone una estructura de avance en cuatro etapas sucesivas pero no disyuntas. A continuación se puede ver un diagrama con estas etapas.

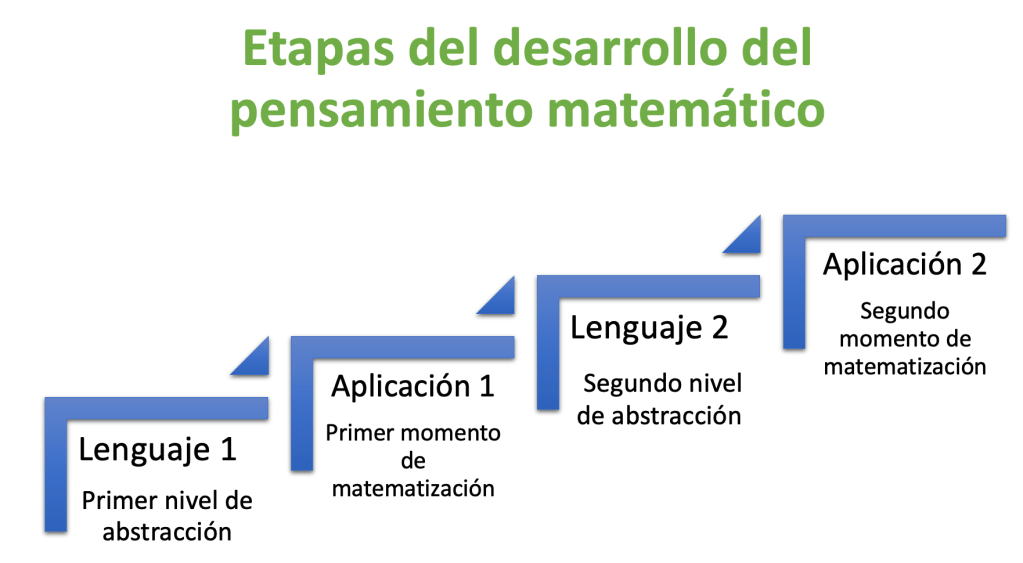
La primera etapa, denominada Lenguaje 1, tiene como objetivo que los estudiantes abstraigan los objetos de la realidad sensible en ideas matemáticas. Esta abstracción se logra con base en procesos de pensamiento generales como: observación, identificación, clasificación, comparación, relación, etc., y procesos de pensamiento matemático (asociados a cada uno de los cuatro ejes de pensamiento matemático, a saber: numérico, variacional, métrico y geométrico), como: conteo, predicción, medición, descripción, ubicación, etc.

La segunda etapa es la de Aplicación 1. Esta es una de las dos etapas dirigidas hacia el desarrollo de la competencia de matematización. En esta etapa, los estudiantes aprenden a resolver situaciones problema matematizables (SPM) que están enmarcadas en cada uno de los ejes de pensamiento matemático, es decir, una situación problema que resuelvan los estudiantes en esta etapa está dirigida a objetos matemáticos incluidos en un solo eje de pensamiento matemático, sin que sea necesario hacer uso de objetos de otros ejes de pensamiento matemático.

En la tercera etapa, llamada Lenguaje 2, los estudiantes tienen un segundo momento de abstracción, esta vez dirigido a re-presentar objetos geométricos como expresiones algebraicas. Este momento es decisivo para el desarrollo del pensamiento algebraico de los estudiantes y se ha mostrado como una de las grandes fortalezas de este paradigma de educación matemática.

Un segundo momento de matematización lo viven los estudiantes en la última de las etapas, Aplicación 2. Esta etapa es similar a la segunda etapa, en el sentido de que también está dirigida hacia el desarrollo de la competencia de matematización, pero se diferencia en que las situaciones problemas que se resuelven aquí presentan integración entre objetos matemáticos de diversos ejes de pensamiento.

Cada una de estas etapas se describe por dos modelos, uno teórico y otro didáctico. El modelo teórico describe los procesos de pensamiento que se desarrollan en cada etapa y el modelo didáctico hace explícita la forma como se desarrollan dichos procesos en las interacciones de enseñanza-aprendizaje. Por ejemplo, el modelo didáctico de las etapas de matematización se describe acá, acá, acá, acá y acá.

Las situaciones de aprendizaje y las situaciones problema que son recursos de estas cuatro etapas del desarrollo del pensamiento matemático están enmarcadas en los cuatro ejes: numérico, variacional, métrico y geométrico, constituyéndose en tensores curriculares para la formación de los estudiantes.